Mapas de Karnaugh

Cuando hablamos de implementar el uso de métodos que permitan simplificar de forma rápida, sencilla y eficiente las funciones algebraicas Booleanas, los Mapas de Karnaugh son una excelente opción. Ya que, una tabla de la verdad se puede convertir en una ecuación de “Suma de productos” o en una de “Productos de suma”. Si quieres conocer más detalles sobre las reglas básicas de simplificación, en las próximas líneas describiremos todo lo que necesitas saber al respecto.

¿Qué son los Mapas de Karnaugh?

Básicamente, los Mapas de Karnaugh son elementos utilizados para que las personas puedan simplificar en gran medida las “Funciones Algebraicas Booleanas”. Dicho método es capaz de reducir los cálculos extensos. Estos mapas también son identificados como “Tabla de Karnaugh”, o “Diagrama de Veitch”.

Todos estos elementos además de la simplicidad que proporcionan en los ejercicios, tienen la capacidad de colocar en buen funcionamiento el cerebro del ser humano. Ya que, estos deben reconocer patrones y otros elementos de expresión analítica, para que los usuarios puedan identificar y eliminar condiciones que se hacen necesarias para la obtención de los resultados.

¿En qué consisten los Mapas  de Karnaugh?

De acuerdo a los expertos en el tema, los Mapas de Karnaugh consisten en representaciones bidimensionales de la tabla de valores de verdades de los elementos que se desean simplificar. Además de ello, se conoce que la tabla de verdad de una función de “N variables”, está compuesta también por 2N filas, mientras que el área del mapa K debe poseer al igual que el anterior 2N cuadrados.

Todas las expresiones que se colocarán en la tabla, se deben organizar en función del peso y siguiendo el “Código Gray” (sistema de numeración binario en el que dos números de forma consecutiva solo se diferencian en uno de sus dígitos), para que solo uno de los números varíe en las celdas cercanas.

Cabe destacar que, cuando inicies la transferencia de números de la tabla de verdad al Mapa de Karnaugh, esta se debe llevar a cabo de forma directa. Allí se puede colocar un 0 o un 1, todo va a depender de la función que tendrá cada una de las filas. Ten presente que, este tipo de mapas también se pueden realizar de manera adecuada con funciones de hasta 6 variables.

En caso de que tengas una mayor cantidad, se recomienda la utilidad de software especializados para dicha función.

Reglas básicas para la elaboración de los Mapas de Karnaugh

Una vez que emprendas la construcción de los Mapas de Karnaugh, debes tener presente que deberás respetar unas reglas básicas para que la elaboración del mismo quede de forma adecuada. Es por ello, que a continuación te destallaremos dichas normas simples que debes tener en cuenta:

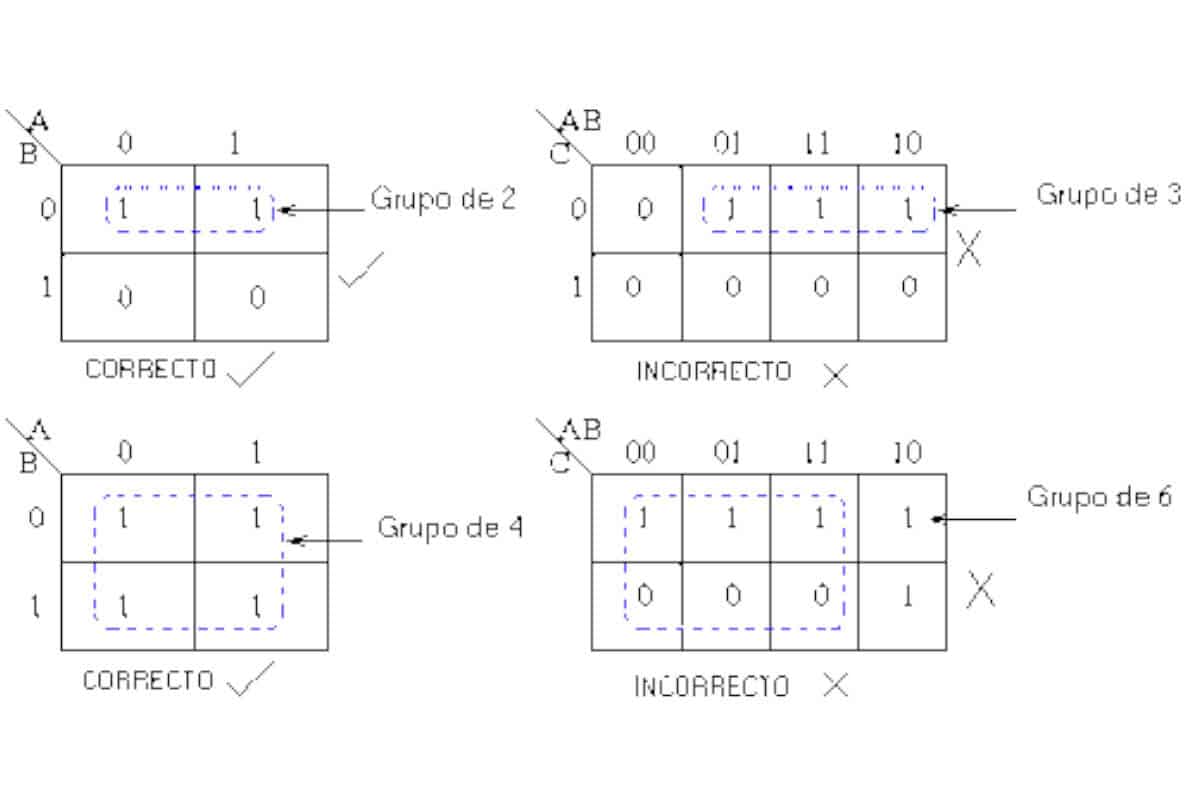
1. Cuando se inician las agrupaciones, el número o el término que se debe considerar de manera primordial es el número 1.
2. Al realizar las agrupaciones, estas solo se realizan de manera vertical y horizontal.
3. Las agrupaciones deben contener 2N de elementos. En otras palabras, se puede decir que las agrupaciones en cada uno de los grupos debe estar conformada por 1, 2, 4, 8 y más 2N, que es la cantidad de números 1 que la conformarán.
4. Si quieres tener una simplificación mayor, debes considerar agrupar la mayor cantidad de números posibles.
5. En la tabla debes considerar todo número 1 que allí aparezca. Cabe destacar que, aquí tienes la posibilidad de unir varios grupos de 1.
6. La formación de los grupos también se puede llevar a cabo a través de las celdas extremas que se observan en la tabla.

Por último, es indispensable considerar la menor cantidad de agrupaciones, siempre y cuando estas obedezcan las reglas que se han expuesto en las líneas anteriores.

Pasos para la ejecución de los Mapas de Karnaugh

Si quieres obtener los resultados adecuados en la elaboración de los Mapas de Karnaugh, es indispensable que luego de tener claridad sobre las reglas básicas a seguir, cumplas con los siguientes pasos:

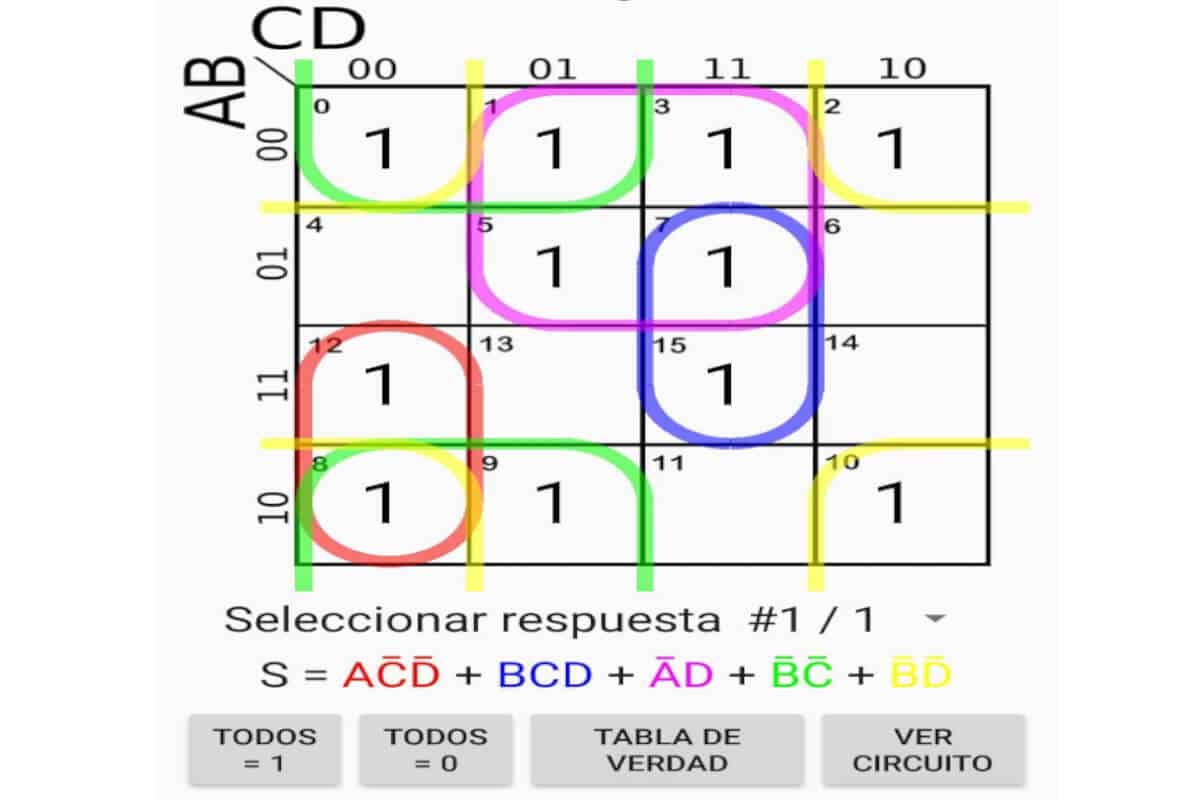
1. Comienza por colocar en una tabla lógica las variables denominadas ABC (por ejemplo).
2. Luego de ello, podrás observar que la lógica digital te proporcionará el resultado “Y” que estás necesitando.
3. Cuando aprecies los valores que son bastante voluminosos, podrás simplificar con Mapas de Karnaugh, llevando los valores de la tabla mapa y ubicando cada 1 de la función “Y” en la coordenada que le corresponde. 
4. Al definir las coordenadas de la matriz y las variables, estas deben ser complementarias. Para ello, debe marcar las negadas con una línea en la parte superior, o simplemente colocando una comilla.
5. A la matriz se llevan las variables ABC de la tabla que corresponde, con el valor más elevado de la salida “Y“(esto se realiza en sus respectivas coordenadas).
6. Se debe colocar 1 para la coordenada que se hayan nombrado A’BC’, 1 para la ABC’ y 1 para la A’BC (todos estos elementos son definidos con la palabra ‘minterms’).
7. Ahora deberás realizar la simplificación con el Mapa de Karnaugh.
8. Continúa sumando los minterms contiguos, y anula las variables que son complementarias.
9. Posteriormente, en casos particulares la suma de los minterms Z elimina la variable A, que se observa en el área complementaria de la operación.
10. Paso seguido, deberás seguir con la “Operación booleana”, (ten presente que una variable se elimina cuando esta se complementa en las sumas).
11. Por último, la suma de Z y X te dará la combinación abreviada de la variable de la tabla de verdad.

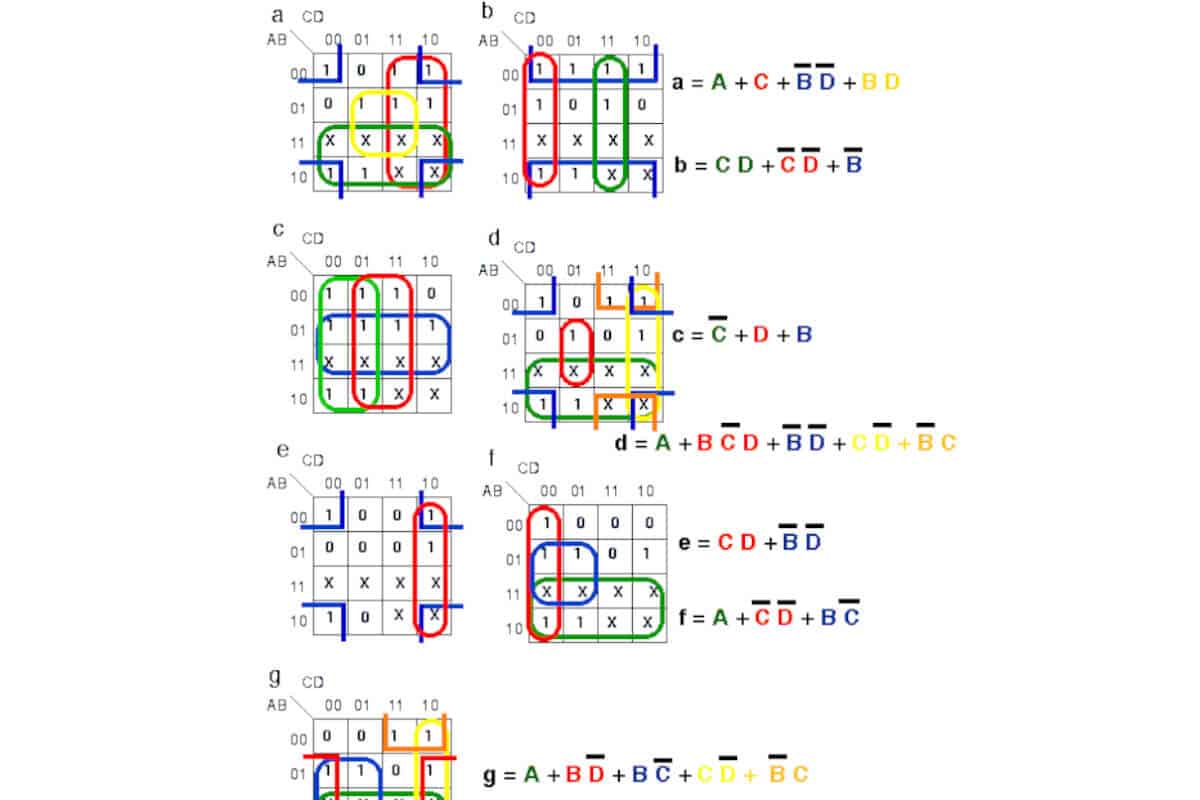
De esta manera, el circuito lógico queda toralmente simplificado y cumple a cabalidad la función que el usuario espera obtener de todo el proceso. No obstante, es posible que al comienzo tengas algunas dificultades para manejar la operación. Sin embargo, con un poco de práctica y desenvolvimiento, notarás que el proceso es mucho más sencillo de que lo que imaginas.

¿Cuáles son las ventajas de los Mapas de Karnaugh?

Ahora que ya conoces las reglas básicas y el procedimiento que debes implementar para ejecutar los Mapas de Karnaugh, es momento de que describamos las principales ventajas que le proporciona a los usuarios la creación de este tipo de mapas. Entre algunas de ellas podemos destacar las siguientes:

• Los Mapas de Karnaugh les proporcionan a las personas la posibilidad de convertir la tabla de la verdad en una ecuación booleana, es decir se transforma en una “Suma de productos” (SOP) o en “Productos de suma” (POS).
• La simplificación se realiza con la utilidad de reglas básicas, que no tienen mayor dificultad para los usuarios.
• La accesibilidad del sistema de simplificación hace que dicho elemento sea mucho más fácil y cómodo de utilizar para las personas. A diferencia de los demás métodos de simplificación en el Álgebra de Boole que se pueden encontrar en la actualidad.
• Este método de simplificación, se trata de una variedad de cuadrados, en donde la expresión obtenida será la mínima.

Dicho todo esto, es momento de que te tomes el tiempo necesario para que puedas construir los Mapas de Karnaugh y simplificar las operaciones de las funciones algebraicas Booleanas que más estés necesitando.